Построение и анализ гибридного РК-метода

- Автор:
Щур, Ольга Федоровна
- Шифр специальности:
01.01.07
- Научная степень:
Кандидатская
- Год защиты:
2002
- Место защиты:
Новосибирск
- Количество страниц:
69 с.
Стоимость:
700 р.250 руб.
до окончания действия скидки
00
00
00
00
+
Наш сайт выгодно отличается тем что при покупке, кроме PDF версии Вы в подарок получаете работу преобразованную в WORD - документ и это предоставляет качественно другие возможности при работе с документом
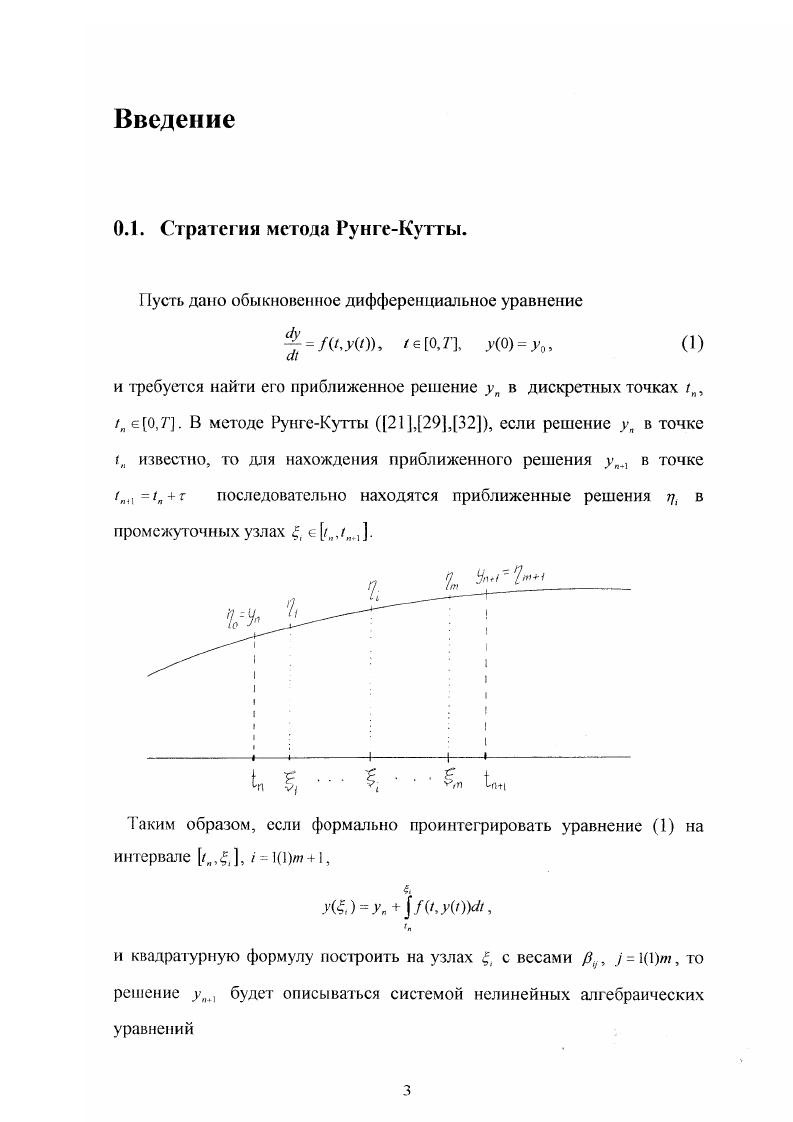
Страницы оглавления работы

Рекомендуемые диссертации данного раздела
| Название работы | Автор | Дата защиты |
|---|---|---|
| Метод конечных элементов для задач конвекции-диффузии с преобладанием конвекции | Карепова, Евгения Дмитриевна | 1999 |
| Проекционно-сеточные методы для решения нелинейных эллиптических задач с дифференциальными операторами векторного анализа | Юлдашев, Олег Ирикевич | 2010 |
| Границы устойчивости разностных схем | Ильютко, Виктор Петрович | 2007 |