Теория автоматизации проектирования объектов и процессов на основе методов конструктивного геометрического моделирования

- Автор:
Волошинов, Денис Вячеславович
- Шифр специальности:
05.13.12
- Научная степень:
Докторская
- Год защиты:
2010
- Место защиты:
Санкт-Петербург
- Количество страниц:
365 с. : ил.
Стоимость:
700 р.250 руб.
до окончания действия скидки
00
00
00
00
+
Наш сайт выгодно отличается тем что при покупке, кроме PDF версии Вы в подарок получаете работу преобразованную в WORD - документ и это предоставляет качественно другие возможности при работе с документом
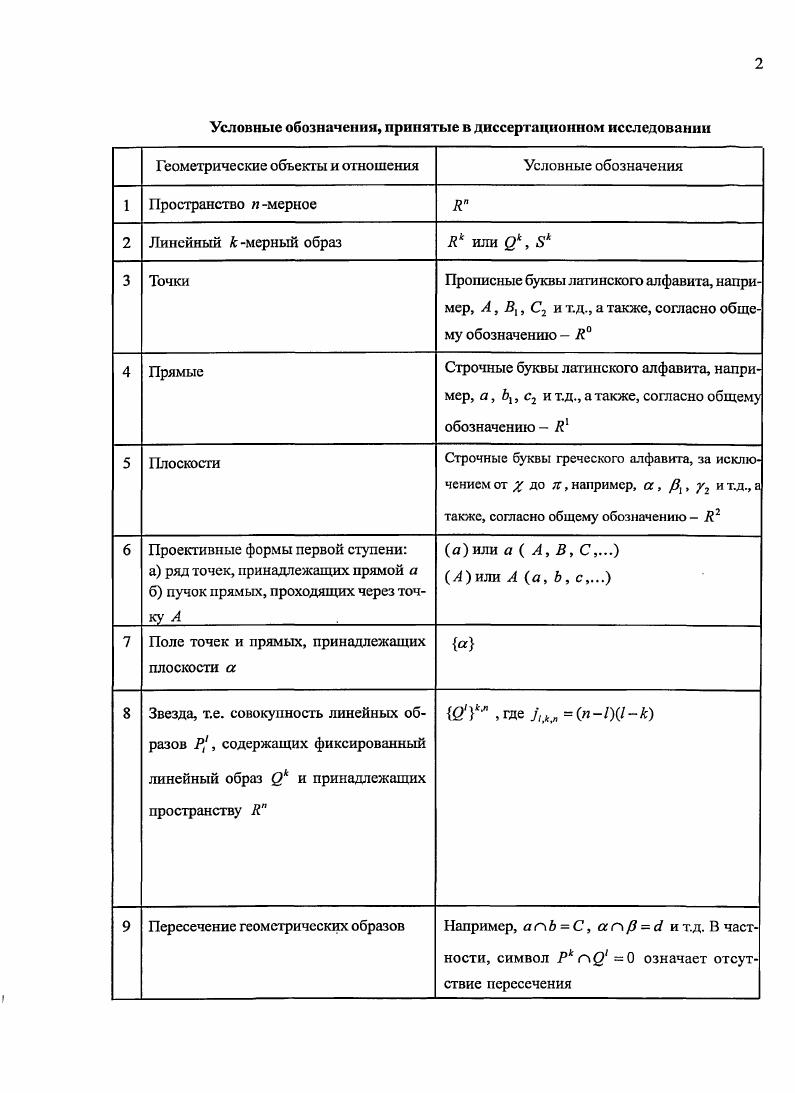
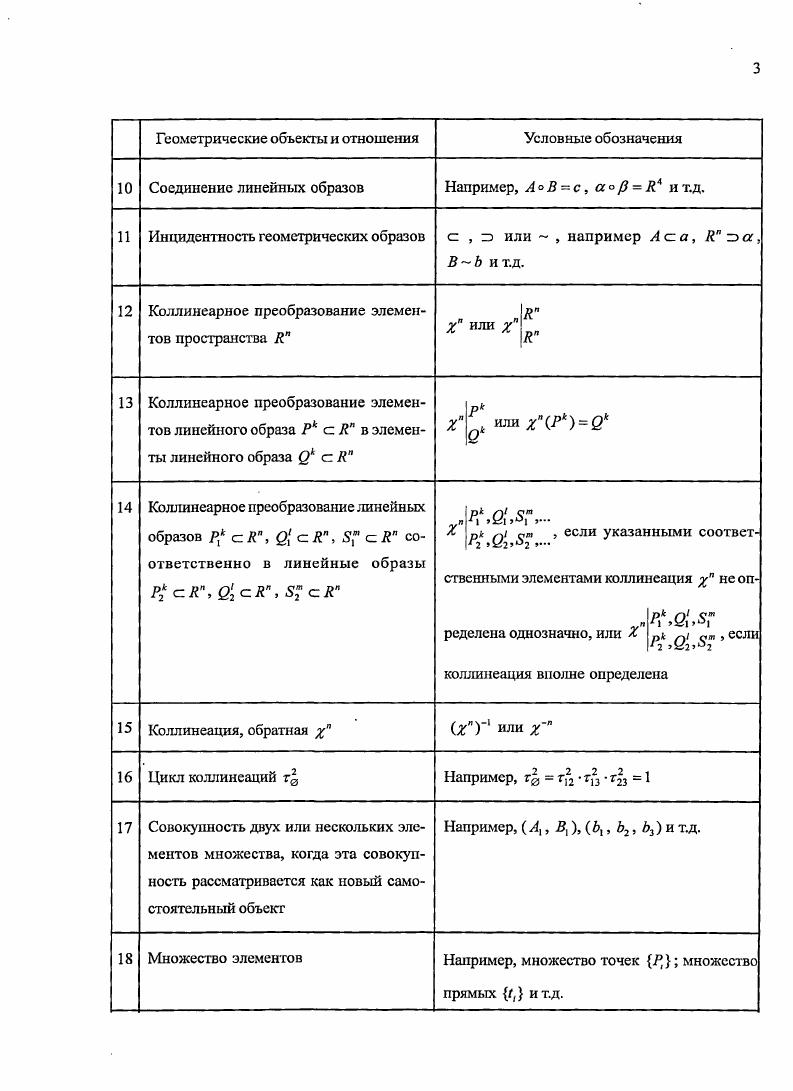
Страницы оглавления работы
Рекомендуемые диссертации данного раздела
| Название работы | Автор | Дата защиты |
|---|---|---|
| Система автоматизации проектирования устройства управления гидрообъемной трансмиссией цепного траншейного экскаватора | Суковин, Михаил Владимирович | 2010 |
| Создание инструментальной среды структурного синтеза объектов | Уржумов, Никита Александрович | 2007 |
| Проектирование гильотинного раскроя листового и рулонного материала с использованием послойных алгоритмов | Сиразетдинов, Тимур Маратович | 2004 |